To assess the potential of CDR technologies and systems, we must first define what constitutes negative emissions and how we evaluate the system boundaries, cost, and net carbon balance of such systems. According to a 2019 paper by Tanzer and Ramírez, there are four main criteria that qualify systems as carbon dioxide removal (Tanzer and Ramírez, 2019).

1. Greenhouse gases are removed from the atmosphere. 

2. The removed gases are stored out of the atmosphere in a manner intended to be permanent.

3. Upstream and downstream greenhouse gas emissions associated with the removal and storage process, such as emissions from land use change, energy use, unintended emissions from industrial processes (fugitive emissions), gas fate, and co-product fate, are comprehensively estimated and included in the emission balance.

4. The total quantity of atmospheric greenhouse gases removed and permanently stored is greater than the total quantity of greenhouse gases emitted to the atmosphere.

A CDR system must meet these four criteria. In addition to CDR systems, there are systems that either avoid emissions or reduce carbon dioxide emissions (Sutter et al., 2019). These systems are commonly confused with CDR systems. Technologies that avoid emissions may produce lower emissions than a reference system delivering an equivalent product or service. Take, for example, the application of carbon capture and sequestration (CCS) to an existing gas-fired power plant. In this scenario, carbon capture reduces the amount of CO₂ emitted from the power plant per unit of electricity generated, but increases emissions upstream (due to increased fuel use) and downstream (through transport and storage of CO₂) (Cuéllar-Franca and Azapagic, 2015). This results in net emissions reduction (or avoidance of emissions) since the power plant with CCS emits significantly less CO₂ per unit of electricity generated, than the same plant without carbon capture. However, even with CCS, this system still results in net emissions to the atmosphere. Therefore, this application of CCS is not classified as a CDR system. 

Within the energy sector, there are technologies that result in essentially zero CO₂ emissions during electricity generation. For example, solar and wind electricity do not emit CO₂ to the atmosphere during use. However, these technologies do not remove CO₂ or other greenhouse gases from the air. Additionally, PV cell and wind turbine manufacturing creates emissions, which must be accounted for. Therefore, these systems are not classified as CDR systems, either.

Finally, it is possible to implement net-zero CO₂ emissions processes, which remove as much CO₂ from the atmosphere as they emit over their lifetime (Hertwich et al., 2015). As an example, the production of a liquid fuel from biomass could be carbon-neutral with the implementation of CCS. The biomass feedstock inherently contains carbon dioxide removed from the atmosphere via photosynthesis. Converting the biomass to fuel could capture and store some of that carbon dioxide. The storage of atmospheric CO₂ from the biomass feedstock has the potential to offset emissions associated with the energy required to convert the biomass to liquid fuel, or the CO₂ emitted elsewhere in the supply chain (e.g., production of fuel conversion and processing facilities). To emphasize the importance of system boundaries on negative emissions, Section 4.1.5 contains an example of a liquid solvent-based approach used for direct air capture, where the captured CO₂ is ultimately stored in an underground geologic formation.

Life cycle analysis (LCA) is a compilation and evaluation of the inputs, outputs, and potential environmental impacts of a product system throughout its life cycle (The International Standards Organisation [ISO], 2006). LCA can provide insight into the resources that are necessary to create and maintain a functioning system, as well as the quantification of GHG emissions that are allocated to each resource (Hellweg and Canals, 2014; Sick et al., 2019). This includes energy resources, materials, water, and land use, amongst others. While the data needed for adequate LCA vary widely for different types of CDR systems, important examples are listed below 1: 

• Carbon intensity or embodied emissions of the materials used to construct and maintain the system;

• Energy resources consumed to construct and maintain the system;

• Energy resources consumed to operate the system, including electricity and thermal energy. In both cases the ultimate source of that energy must be considered; for thermal energy, required temperature is an important parameter;

• Water requirements to construct, maintain, and operate the system;

• Land required to operate the system;

• Mineral requirements to construct, maintain, and operate the system;

• Chemical requirements to construct, maintain, and operate the system;

• Carbon-intensity of materials or embodied emissions; 

• Albedo effect (if any) from the construction, maintenance, and operation of the system; and

• Impacts on CO₂ storage and likely storage duration.

Life cycle analyses help us understand the potential trade-offs involving a system’s impacts and identify these elements of the system (the so-called hot spots) that contribute most to its environmental performance. For a CDR system, much of the emphasis of the LCA is on understanding the greenhouse gas impacts of the technology, as an LCA determines if the system successfully removes more CO₂ from the atmosphere than it produces. In this case, the impact of interest is the greenhouse gas emissions, which is the focus of many greenhouse gas accounting protocols. However, a CDR system operates within a wider socioeconomic context, affecting resource, water, and energy consumption and land use. Therefore, it is necessary to consider system impacts holistically to understand CDR systems and trade-offs (e.g., greenhouse gas emissions; water consumption; and toxicity to animals, plants, and ecosystems). For example, one CDR system may remove the most CO₂eq but have a major impact in another category, such as mineral, land, or water requirements. Given that preventing climate change will be balanced against other important goals (e.g., reducing poverty, protecting biodiversity), incentivizing CDR may not be limited to the effectiveness of CO₂ removal (United Nations, 2020; see Section 1.6). Additionally, if two processes have similar impacts in terms of net CO₂eq removed, other factors such as land or water intensity may determine that one system is preferable to the other, in addition to the impact assessment methods used to estimate such factors (Yang et al., 2020). 

Since LCA accounts for CO₂eq emissions within chosen boundary conditions, suitable boundary conditions must be chosen to correctly evaluate CO₂eq emissions over the technology life cycle. Potential inputs, outputs, and CO₂eq emissions are outlined in Figure 4.2. Here, the inputs and outputs are generalized to provide a technology-agnostic overview. Not every input and output is present for each CDR approach. 

Within many greenhouse gas accounting protocols, emissions fall within three classes: direct emissions, indirect emissions, and embodied emissions. Direct emissions are those that are directly controllable and produced from within the system boundary (Section 4.1.2). For example, CO₂eq emissions from an on-site combustion unit are considered direct emissions. Indirect emissions occur as a result of system activity but do not occur within the system boundary. For example, a system that uses grid electricity does not directly produce the emissions associated with electricity, but does contribute to the demand for electricity, resulting in emissions during power generation. Finally, embodied emissions are those that result from the production and use of any good or the provision of any service (e.g., the emissions embodied in materials and equipment used by the system, or any product resulting from the system). These emissions are incurred either once (for most capital equipment, excluding replacements) or repeatedly throughout the system’s lifetime (for most operating equipment or items that are repeatedly purchased). For example, the embodied emissions of steel used for a reactor include emissions associated with acquiring the raw materials, processing, manufacturing, transportation, and energy used in steel production. While common in greenhouse gas accounting, direct, indirect, and embodied emissions terminology is not frequently used in LCA literature because the meaning depends on the system boundaries for any given assessment.

The Greenhouse Gas Protocol is a commonly used method for reporting GHG emissions that was developed by the World Resources Institute (WRI) and the World Business Council for Sustainable Development (WBCSD). Within this framework, direct emissions are referred to as “Scope 1,” indirect emissions from the purchase of generated energy are referred to as “Scope 2,” and embodied emissions (as well as other related emissions) are referred to as “Scope 3.” Because different frameworks for an LCA are used by different analyses, this terminology sometimes causes confusion (Greenhouse Gas Protocol, 2020).

An LCA can be used to determine a system’s net emissions/removal of CO₂eq from the atmosphere. Using Figure 4.2, this corresponds to the total CO₂eq input minus the total CO₂eq output and any other CO₂eq emissions (orange arrows). This can also be represented as the ratio of all the emissions from a system to all of the CO₂ removed from the atmosphere by the system. If this ratio is greater than 1, the system emits more CO₂eq than it removes and is not considered a CDR system.

System boundaries delineate what is included and what is excluded in a given analysis. The system boundary is not necessarily a geographical boundary (i.e., on-site vs. off-site), but rather a boundary designed to identify all components required to operate the CDR approach. Here, we discuss the three main types: (1) gate-to-gate, (2) cradle-to-gate, and (3) cradle-to-grave 2. These three system boundaries are displayed for a generic CDR approach in Figure 4.3. A gate-to-gate analysis assesses only one distinct phase (e.g., crude oil refining, copper smelting). A cradle-to-gate analysis includes all of the process steps and associated flows between extraction of a natural resource (e.g., crude oil, copper ore) and production of a finished product (e.g., diesel fuel, a microprocessor). Cradle-to-grave extends this analysis to include the use (e.g., combustion of a fuel, calculations by a computer) and disposal (e.g., landfill, recycling, combustion) of a finished product. Since carbon dioxide emissions can occur anywhere in the system (from extraction to production to final use), a cradle-to-grave analysis can determine if a defined system truly results in negative emissions. 

Many product systems are multifunctional: They produce more than one product. This occurs with many carbon capture and utilization systems, including BECCS and CO₂-to-fuels. Assessing multifunctional systems requires dividing up the environmental impacts of the process between the co-products based on their allocation. The International Standards Organisation (ISO) states: “Wherever possible, allocation should be avoided by: 1) dividing the unit process to be allocated into two or more sub-processes and collecting the input and output data related to these sub-processes, or 2) expanding the product system to include the additional functions related to the co-products….” (2006). The first point in the ISO quote indicates that what is viewed as one complete system may be composed of multiple subsystems. In some cases, these subsystems can operate independently of one another, allowing focus on the specific sub-process of interest to perform the LCA. However, multifunctional processes usually cannot be subdivided into independent sub-processes that eliminate the need for allocation. The second point in the ISO quote above refers to the process of system expansion, in which system boundaries are expanded until they encompass the impacts of what would otherwise be co-products. System expansion allows for allocating those impacts to one product, eliminating the need for allocation methods that divide the impacts of the process across multiple co-products. In other words, the system expansion method displaces emissions from its co-products compared with conventional energy production and credits them to the specified product (Nguyen and Hermansen, 2012). This method is used when separation is not possible or meaningful. An example is the co-production of electricity in a steam methane reforming hydrogen production plant. When comparing their performance to alternative hydrogen production systems, the boundary of the alternative system has to be expanded to include electricity production, e.g., by a natural gas-fired power plant (Antonini et al., 2020). 

Allocation methods distribute the environmental impacts of the system to products through the use of a functional unit (Kolosz et al., 2020). The functional unit provides a quantified performance of the product system for use as a reference unit (Rebitzer et al., 2014). This means a) that the functional unit provides the reference on which inlet and outlet flows of the system are based, and b) that the unit itself is relevant and specific to the type of system being analyzed. 

Allocation methods can include physical allocation (by mass or volume) (Guinée et al., 2002), energy allocation (Luo et al., 2009), and market or economic allocation (Guinée et al., 2002; Kolosz et al., 2020), among others. Each method partitions the impact of the system among the co-products in different ways.

• Physical (or mass, or volume) allocation: The physical allocation method distributes inputs and outputs from the system to the co-products based on their mass or volume. In the literature, physical allocation is best applied when there are limited co-products. Additionally, if one co-product has a service in terms of energy (i.e., fuel) and the other product is valuable in terms of mass (i.e., plastic), it does not make sense to use physical allocation.

• Energy Allocation: The energy allocation method assesses performance from the perspective of the effort required to produce a product. For a system meant to capture CO₂, the effort may be measured in Megajoules (MJ) required per tonne of CO₂ captured (Nguyen and Hermansen, 2012; Pradhan et al., 2011; Wang et al., 2004). If the main product of an LCA is mass-based only (e.g., tonnes of CO₂ removed) energy content would not be used directly on CDR systems, and instead, mass or other allocation methods should be used.

• Market (or economic) allocation: In market or economic allocation, the inputs and outputs are distributed to the co-products based on their market value (Zimmermann et al., 2018). All feedstocks have costs that fluctuate, depending on supply and demand (Luo et al., 2009). Market allocation essentially operates in two distinct modes: fixed and non-linear. Some parameters may or may not be constants but consist of marginal data that can be predicted through time.

• Exergy allocation: The exergy allocation method distributes the impact of the system to the co-products based on their exergy (i.e., the maximum theoretical work as defined by the second law of thermodynamics). 

For example, take a polygeneration plant that (1) uses biomass to produce electricity, capturing the CO₂ from the combustion process, (2) uses part of the captured CO₂ for urea production, and (3) geologically stores the remainder of the CO₂. This results in two co-products from the system for which the impacts of the process are divided: electricity and urea. This system has the additional benefit of geologically storing CO₂, which can be credited to the two products. The electricity and urea production system cannot be broken up into subsystems that do not require allocation. System expansion could be used to compare this system to traditional energy systems, which would be the preferred choice. Since electricity is produced in units of energy (typically megawatts), while urea is commonly used as fertilizer and sold in units of mass, mass and energy allocation are not preferred. Market allocation could be used to allocate to the electricity and urea proportional to their market price. 

As seen above, different allocation methods can produce conflicting results, and care must be taken when selecting and applying them to CDR systems. If allocation is used, then it is advantageous to use more than one allocation method to evaluate the results. A related discussion of the carbon footprint of CO₂ capture further illustrates the importance of choosing a suitable approach for the boundary conditions (Müller et al., 2020).

One of the biggest challenges associated with LCA is data availability and accuracy (Sick et al., 2019). Analyses typically use extensive amounts of data to gather and analyze information related to the carbon footprint, environmental impacts, and economic impacts of systems. Inaccurate data or poor data resolution can lead to greater LCA uncertainty, so it is imperative to complement any LCA with a sound and suitable uncertainty analysis (Fernández-Dacosta et al., 2017; Mendoza Beltran et al., 2018). Because there are several inputs in an LCA, ensuring that data are as accurate as possible is crucial to avoiding compounding uncertainty (Bamber et al., 2020; Lima et al., 2020; Heijungs and Huijbregts, 2004). Parameter uncertainty (also known as data uncertainty) can be quantified through established uncertainty methods, such as statistical methods or Monte-Carlo analysis (Baek et al., 2018; Heijungs, 1996; Maurice et al., 2000). However, other areas of uncertainty, such as scenario uncertainty and knowledge base uncertainty, 3 are more difficult to address, but methods are being developed to evaluate these as well (Fernández-Dacosta et al., 2017; Mendoza Beltran et al., 2018). Generally, the more mature a technology is, the more reliable the associated data for LCA.

Choosing a reference system is another challenge associated with LCAs. The reference system is the incumbent system compared with the new product system, on which the LCA is being performed. The reference system allows for comparison of environmental impacts. The choice of reference system plays a large role in assessing the environmental impact savings for the system, and therefore impacts the results of the LCA. For CDR, few of these approaches are deployed today. This provides a challenge when selecting a reference system, as there is not a similar reference system for comparison.

The permanence of CO₂ removal is an additional and important consideration for life cycle analyses. CO₂ can be safely stored deep underground for hundreds to millions of years and with no or little meaningful leakage – the result effectively being permanent storage (Alcalde et al., 2018). Because these systems remove excess CO₂ from the atmosphere and store it “in a manner intended to be permanent,” they meet the second criterion for CDR presented at the beginning of this section. In other cases, especially those involving biological systems, the durability of carbon storage is limited, in some cases to decades or less, due to both physical risks and socioeconomic factors. The climate benefits of these systems will be limited compared to permanent storage, and these differences must be accounted for in LCA and any other analysis (Herzog et al., 2003; Levasseur et al., 2010, 2012). See Chapter 1 for a more complete discussion of permanence. 

Further, LCA for newly-proposed CDR systems or approaches with low technology readiness levels (TRL) also proves challenging (See Figure 4.4). Low-TRL approaches are unproven on an industrial scale and therefore carry large inherent uncertainty surrounding system impacts. This uncertainty is compounded by limited data on these approaches. While LCAs of low-TRL systems increase uncertainty, these analyses can be very helpful in determining areas for improved environmental impact (Moni et al., 2020). 

A final challenge for LCA analyses is the lack of common guidelines for such analyses, specifically with respect to low-TRL technologies. To compare the potential for negative emissions across technologies, LCAs must be performed with analogous system boundaries. This proves difficult when comparing, for example, technological and biological systems. Currently, various initiatives provide guidance in harmonizing the application of LCA. For example, the World Resource Institute and the Greenhouse Gas Protocol developed a set of guidelines on how to account for greenhouse gas emissions and carbon dioxide removal from land use, land use change, bioenergy, and related topics (Greenhouse Gas Protocol, 2020). In another example, a report by Zimmerman et al. (2018) provided recommendations on the type of scenario modelling and system boundaries that should be taken into account when CO₂ is used within the system boundary.

Solvent-based direct air capture (DAC) uses chemicals dissolved in water to contact and capture CO₂. The process discussed uses a 1.0 – 2.0M potassium hydroxide solution (KOH(aq)) to capture CO₂ from the air in the contactor unit, forming a potassium carbonate (K₂CO₃(aq)) solution (Keith et al., 2018; NASEM, 2019). The solution is then fed into a precipitation/solid separator unit. Here, anionic exchange occurs between calcium hydroxide (Ca(OH)₂(aq)) and K₂CO₃(aq) reproducing the KOH(aq) solution and precipitate, calcium carbonate (CaCO₃(s)). From here, the KOH can be fed back to the contactor. The CaCO₃ is processed and sent to the calciner to produce CO₂ and calcium oxide (CaO(s)) at temperatures around 900º C. The CaO is fed into the slaker, where it reacts with water to reproduce Ca(OH)₂. The CO₂ is dehydrated in the condenser, then compressed for pipeline transport to geologic sequestration. Figure 4.5 demonstrates this process.

This process has large power requirements, ranging from 300 – 500 MW at a scale of 1 million tonnes of CO₂ removal per year (NASEM, 2019). These power requirements include both electrical and thermal energy, as outlined in Figure 4.3. To date, the thermal energy requirements have been evaluated exclusively by the use of an oxy-fired calcination unit fed with natural gas. Future systems may utilize electricity to meet these thermal energy demands and therefore could use low-carbon resources such as wind, geothermal, and solar energy. 

In this example, we compare the CO₂eq emissions from using dedicated, stand-alone energy facilities to provide the steady 300 MW of power (work and heat) required for solvent-based DAC. The DAC facility is kept operational 90 percent of the time to prevent repeated start-up and shutdown costs associated with the calciner. To assess the negative emissions potential of the DAC approach, direct and embodied emissions for each part of the process should be considered when determining the net removal of CO₂ from air. 

For the solvent-based DAC system, there are many different energy resources and configurations that can power the process, assuming the availability of electric calcination units. Figure 4.6 outlines five distinct cases in which different energy resources are used to power the DAC process. We consider two DAC configurations coupled to different energy resources: a natural gas-fired calciner directly heated with natural gas, and electric resistance calciners that use resistance heating and electricity from solar photovoltaic (PV), nuclear, wind, and geothermal power (McQueen et al., 2021). Each of these processes includes direct emissions, indirect emissions, and embodied emissions for the capture process, compression to pipeline pressure, transport via pipeline, and ultimate injection into geologic reservoirs deep underground for permanent storage. The direct emissions include emissions from combustion units, CO₂ resulting from chemical reactions, or other emissions that result directly from chemical reactions. Here, emissions from energy production are included in direct emissions, as the system studied contains both the DAC system and the power system. However, in cases where the power source is outside of the system bounds, these would be considered indirect emissions associated with energy consumption. One example of the embodied emissions for this DAC system is the total amount of emissions resulting from manufacturing, transporting, and installing the components required to construct the system, such as the air contactor and calciner.

The natural gas pathway presented here utilizes an oxygen-fired calciner where the natural gas is combusted within the kiln, in direct contact with calcium carbonate. The primary direct emissions occur as a result of combustion of natural gas. In this case, all CO₂ emissions from natural gas combustion inside the calciner are co-captured with the CO₂ from air; however, only 90% of the emissions from natural gas-based electricity generation are captured. Additional emissions are embodied within the materials used to perform the process, as noted above. When evaluating natural gas-based systems, there are additional upstream embodied emissions considerations due to methane leakage (i.e., fugitive emissions). Estimates of methane leakage are uncertain but, here, values from Alvarez et al., (2018) are considered. Most embodied natural gas emissions come from recovering natural gas at extraction sites, accounting for 3.5 (Environmental Protection Agency, 2017) – 7.6 (Alvarez et al., 2018) Mt of methane emitted per year from the U.S. oil and natural gas supply chain. The second-largest source of embodied emissions is the transportation of unprocessed natural gas from the production site to the processing site, with 2.3 (Alvarez et al., 2018) Mt - 2.6 (Environmental Protection Agency, 2017) of methane emitted per year from the U.S. oil and natural gas supply chain. Within the embodied emissions, pneumatic controllers and equipment leaks make up the largest emissions sources in the oil and natural gas supply chain. Malfunctioning controllers are the major contributor to pneumatic controller emissions (Alvarez et al., 2018). Emissions also occur during processing, transmission and storage, distribution, and oil refining and transportation.

Embodied natural gas emission values are important because methane has a higher global warming potential (GWP) than CO₂ with a GWP20 of 86 and a GWP100 of 28. The impact of methane emissions illustrates the importance of including non-CO₂ greenhouse gas emissions in the analysis and demonstrates the impact these emissions can have on the overall emissions footprint of the process (Environmental Protection Agency, 2019). This impact can be seen in Figure 4.6 for natural gas, as it has the largest direct and indirect embodied emissions of any alternative energy resource coupled to DAC.  

The second pathway presented in the figure is solar energy. Here, there are no direct emissions caused by the energy source. Instead, all the emissions are embodied in the process materials, their production, and embodied energy. Solar is an intermittent energy resource with a capacity factor 4between 24.1 percent (seasonally adjusted) and 35.2 percent (best-in-class) (Honsberg and Bowden, 2014; NREL, 2019). This indicates that a significant amount of energy must be stored to keep the solvent-based DAC facility continuously operational (assuming it does not also use grid-supplied electricity). Conventional energy storage infrastructures (in this case, lithium-ion batteries) have large embodied emissions associated with their production. Therefore, while a solar-powered DAC system has no direct emissions, the embodied emissions of the energy system that must be coupled to the DAC plant may significantly increase the system’s emissions (Figure 4.6). Similarly, the wind scenario uses a best-in-class capacity factor of 52 percent (NREL, 2019). Since the goal of this analysis is to avoid intermittency in energy supply when operating the DAC facility with a dedicated energy facility, this system requires similar energy storage infrastructure, which contributes to the embodied emissions of the integrated system. 

Like the previous scenarios, a nuclear energy-powered DAC facility does not have direct emissions associated with capturing carbon dioxide. This energy resource also has a capacity factor that can keep the DAC facility continuously operational without requiring energy storage (U.S. Energy Information Administration, 2019). This further reduces the embodied emissions associated with the system, resulting in the lowest-emissions option presented here. This is primarily because nuclear facilities can supply energy to DAC operations 90 percent of the year with no direct emissions. Despite these benefits, nuclear energy opponents cite high costs, long construction lead times, hazardous nuclear waste, and the risk of nuclear weapon proliferation as reasons to avoid this energy source.

The final energy scenario uses geothermal energy to power a solvent-based DAC facility. Like nuclear facilities, geothermal facilities can supply continuous energy to the DAC facility without the need for energy storage infrastructure, reducing the embodied emissions. However, the geothermal scenario includes CO₂ emissions associated with the recovery of geothermal energy, which vary by location (Section 3.3.2 in Chapter 3). Direct emissions from geothermal energy production occur as a result of the working fluid produced from the Earth. These working fluids supply heat to the geothermal facility that is used to turn a turbine and create energy. However, geothermal working fluids contain dissolved gases, primarily CO₂, producing average emissions of 7.71 kgCO₂/mmBTU for unmitigated operations (U.S. Energy Information Agency, 2016).

After it is captured, the CO₂ is compressed for transportation (via pipeline, truck, or ship). For the DAC process to result in negative emissions, the CO₂ must be removed from the atmosphere in a manner intended to be permanent. Geologic storage of CO₂ in sedimentary formations deep underground, such as saline aquifers and depleted oil and gas reservoirs, means the DAC facility is part of a DACCS system. As indicated by the hashed bars in Figure 4.6, the amount of CO₂ permanently stored is defined as that removed from the air, minus the direct and embodied emissions from the individual steps required to remove, compress, transport, and inject CO₂ deep underground. Of the five scenarios, DAC powered by nuclear energy coupled to geologic storage results in the greatest net CO₂ removal from the air. Chapter 3 explores worldwide opportunities to site these DACCS systems in a responsible way. Chapter 5 examines alternate fates for DAC-derived CO₂ that provide net carbon dioxide removal from the atmosphere (e.g., beneficial reuse or utilization).

Another relevant consideration for CDR approaches is the cost of the technology. While there are multiple ways to estimate cost, they have much in common (n Rubin et al., 2013). This section focuses on the key components of cost estimates and discusses how, based on these estimates, full techno-economic analysis is undertaken, making use of suitable economic and financial parameters. Many existing analyses focus on the cost, particularly the cost per tonne of CO₂eq removed. However, costs cannot be evaluated in a vacuum, as many environmental and social factors must be considered when evaluating a CDR system, among other conditions that limit the validity of TEA results for developing technologies. 

As in LCA, setting system boundaries is the first step for successful analysis. The TEA and LCA 5 of a CDR system often have different goals and scopes, which lead to different boundary conditions. But, in some cases, LCA and TEA can be performed together, sharing the same system boundaries and criteria. But as previously noted, the system boundary is not necessarily solely geographic. 

The next step is to estimate the cost of building the CDR system or, if the CDR approach involves agriculture, any upfront investments required to change practices. These costs are colloquially called the capital expenditure (CAPEX) of the technology, and represent all fixed, one-time expenses. For engineering solutions, the capital cost of the system includes any initial investment in core equipment and components (inside battery limits, or ISBL), as well as engineering fees and the supporting buildings or other infrastructure required to connect the plant to the outside world. Handbooks are available for the capital costing of processing plants (e.g., Gerrard, 2000; Peters et al., 2003; Towler and Sinnot, 2013), as well as dedicated works and guidelines from, for example, the CO₂ capture and storage literature (DOE/NETL, 2015; Sintef energy research, 2017; Van der Spek et al., 2019; van der Spek et al., 2017a, 2017b). The sum of all capital investment may be called the Total Capital Requirement (TCR), which represents the total initial investment that will be necessary to deploy the technology, including the cost of financing the technology and any contingencies during development and construction (Rubin et al., 2013). 

Many costing studies, however, do not aim to present the absolute capital cost, but rather the cost on a per-tonne-CO₂-stored basis (the so-called specific capital costs). This makes it possible to determine the most “carbon-efficient” use of a limited amount of capital: in other words, the optimal allocation of capital to maximize CO₂ removed. To determine the capital cost on a per-tonne-CO₂-captured basis, the capital cost of the system must be annualized. There are multiple ways to do this, but a simple initial methodology involves using a capital recovery factor (CRF): the amount of capital cost “recovered” per year (Rubin et al., 2013). This can also be thought of as repayment of capital borrowed to build the project. The CRF is based on the economic lifetime of the project (in years) and the discount rate, both of which have a large impact on the resulting annualized capital costs. The discount rate reflects the risk of the investment, represented as a cost of capital, including both the interest rate on borrowed funds and the returns expected by investors. In this case, the discount rate is the weighted average cost of capital (WACC). From this information, the CRF can be determined via the following equation.

In this equation, the symbol i represents the discount rate (between 0 and 1) and the symbol n is the CDR plant’s economic lifetime in years 6. Since the discount rate depends on the riskiness of a project, it may vary substantially among investments. For example, the discount rate charged for capital for an innovative, first-of-a-kind (FOAK) technology will be much higher than the discount rate for a widely deployed, lower-risk technology. The total capital cost of the system multiplied by the CRF gives the annualized capital cost of the system. Once the annualized cost of the system is determined, it can be divided by the annual amount of CO₂ captured to determine the capital cost of the system on a per-tonne-CO₂-captured basis.  

As an example of the impact of the discount rate and plant lifetime, consider a generic CDR system that costs $10 million to build and is designed to capture 10,000 tCO₂/yr. In Figure 4.7, those two parameters are varied sequentially to show the impact on the annualized capital cost ($/year) on a per-tonne-CO₂-captured basis ($/tCO₂) as these are the preferred cost units. Looking at Figure 4.7, the same capital cost and capture rate can result in annualized capital costs ranging from $50 to $300/tCO₂ over the assumed parameters. Therefore, it is important to carefully consider which parameters are used throughout the analysis. 

The last common aspect of CDR system costs is the inclusion of operating costs. Operating costs are those incurred during the operation of a system, including energy, chemicals, water, labor, maintenance, and other repeated purchases. These costs vary widely but can be calculated based on the individual requirements of each CDR system. Once the operating costs are determined on a per-year basis, they can also be estimated on a per-tonne-CO₂-captured basis.

There are many challenges when performing techno-economic analyses on CDR approaches. One of the more common challenges is estimating the costs for new or low-TRL approaches. Low-TRL approaches are unproven on an industrial scale and, therefore, carry large inherent uncertainty surrounding system requirements, such as infrastructure, materials, and equipment requirements outside battery limits. Thus, estimating these costs becomes challenging in comparison to existing, high-TRL approaches. Rubin (2019) put forward a method for calculating the cost of advanced CCS technologies that can also be useful in the context of CDR approaches. He applied a hybrid method of cost escalation from low-TRL approaches to FOAK plants, with subsequent cost reduction due to technological learning by repeated manufacturing, deployment, and operation (Section 2.2.4). However, the cost increase from a low-TRL technology to a FOAK plant, and to a lesser extent the technological learning rate after the first plant, are difficult to quantify, leading to high error margins of the final hybrid cost estimate. Van der Spek et al. (2017a) showed error margins of -60 percent to +100 percent for a TRL 3 CO₂ capture technology when using Rubin’s methodologically suitable hybrid costing approach. That was double the uncertainty margins of the standard, but methodologically unsuitable, bottom-up costing approach (-30 percent to +50 percent). Although cost changes are difficult to estimate, it has been empirically observed that costs go up between early, low-TRL estimates and actual, as-built first-of-a-kind costs. Performing TEAs on low-TRL technologies necessarily increases uncertainty in the analysis. This is normal, and we advise embracing and communicating these uncertainties is important, as the results might help guide research and/or policy directions and indicate areas that are most likely to lead to more accurate estimates. An international working group under the auspices of the IEAGHG Cost Network recently published a good account of uncertainty analysis methods and guidance on their selection and use (Van der Spek et al., 2020).

Additionally, the cost of materials and energy resources is dependent on location (IEA Greenhouse Gas R&D Programme, 2018). This leads to the creation of location-constrained scenarios where the system cost is specific to a certain location. This is also true of analyses that incorporate tax incentives among other forms of governmental incentives, limiting the validity of these cost estimates to specific geographies.

Finally, system boundaries heavily influence the overall cost of the system. Inclusion or exclusion of various operations in the capital cost and the operating cost may have a large influence on the cost viability of the entire system. In many techno-economic analyses, the technology used to capture CO₂ from the atmosphere is separated from post-processing of CO₂ or acquisition of raw materials. Separating the capture system from post-processing systems can give the cost of CO₂ removed by the capture system, but does not account for downstream costs associated with either storing or utilizing the captured CO₂. This illustrates, again, why is it important to define robust and appropriate boundary conditions. 

In conjunction with the techno-economic analysis methods described above, there are cases during deployment where the concept of “technological learning” may provide important insights for CDR approaches. This concept is based on the empirical observation that many emerging technologies get significantly cheaper per unit over time (Rubin et al., 2007). One of the best-known examples is solar photovoltaic modules, which have fallen in cost by two orders of magnitude over 40 years (Kavlak et al., 2018). Dozens of other technologies in sectors such as chemicals, electronics hardware, and energy have also shown substantial cost declines (Nagy et al., 2013). Notable exceptions do exist, such as nuclear power, where increased scale increases complexity, driving up the costs of the system (Grubler, 2012). It is particularly important to consider potential future cost changes when analyzing policy or investment choices over the medium or long term. 

Examining historical cost declines has shown that many technologies follow an “experience curve” (sometimes called a “learning curve”) pattern, in which the capital cost of producing the next unit of the technology falls in relation to the total (cumulative) stock of the technology that has been produced (Nagy et al., 2013).

Here, y(t) is the inflation-adjusted cost of producing the next unit of the technology at time t, B is the unit cost of the first deployment, x(t) is the total cumulative stock at time t, and w is a (usually positive) exponent related to the rate at which the costs change. The “unit cost” is normalized to a relevant parameter of technology’s capacity, such as MW for electricity generation technology or MWh for energy storage technology. The fractional cost reduction for one doubling of the cumulative production is known as the “learning rate” (LR) (Rubin et al., 2015).

Observed learning rates are usually expressed as a percentage, and they generally range between 5 percent (slower learning) and 30 percent (very fast learning). 

The reasons behind the observed patterns of learning are complex and continually debated. They appear to combine a variety of effects, including simple economies of scale, streamlined and standardized supply chains (e.g., replacing specialty parts with commodity parts, harmonizing and standardizing component sizes and interconnections), and true “learning” by technology designers, manufacturers, installers, and designers about lower-cost approaches to product design, manufacture, installation, and operation. The central conceptual insight of the experience curve approach is that as society gains experience with a technology (using the cumulative production as a proxy for “experience,”) it is typically able to lower production costs. The overall effect is known as “learning-by-doing,” and technologies are said to “move down the learning curve”.

Technology learning theory can be applied to CDR approaches. The relevant units by which to normalize capital costs are tonnes of CO₂ (tCO₂). However, there is very little historical data on the costs of CDR approaches, and no CDR approaches have been produced in a large enough amount to have increased the total cumulative production through several doublings, which is roughly the amount needed to begin reliably observing learning effects. The main challenge, then, is to find representative estimates of the learning rate for various CDR approaches. Despite this, it is still possible to estimate future cost reductions for individual CDR approaches by (a) assuming CDR approach learning rates are likely to fall within the range generally seen with other technologies (proxies), and (b) projecting a future schedule of production (Baker et al., 2020), although these estimates have high uncertainty. 

It is not possible to predict precisely what improvements will occur in production processes and technology designs to lower costs. While history strongly suggests that there will be improvements, with the learning rate representing the net impact of these as-yet-unknown improvements on future costs, over-reliance on technology learning can also be disadvantageous, since this learning is not guaranteed. Because technology learning carries inherent uncertainty in the cost projections of a given technology, using sensitivity analysis can help quantify the uncertainty in a given rate of technological learning, thus increasing the applicability of a given learning analysis (Rubin et al., 2015). An additional challenge to learning theory is the ability to project the true production cost trend of a given technology, as opposed to the market cost, which is non-equilibrium and can be influenced by many market conditions (Rubin et al., 2015; Wene, 2008). 

To determine the cost of net-negative CO₂eq emissions, the base cost of the process can be adjusted to account for life cycle CO₂eq emissions. This means that the cost per-tonne-CO₂eq is converted to the cost per-tonne-CO₂eq net removed using the following expression:

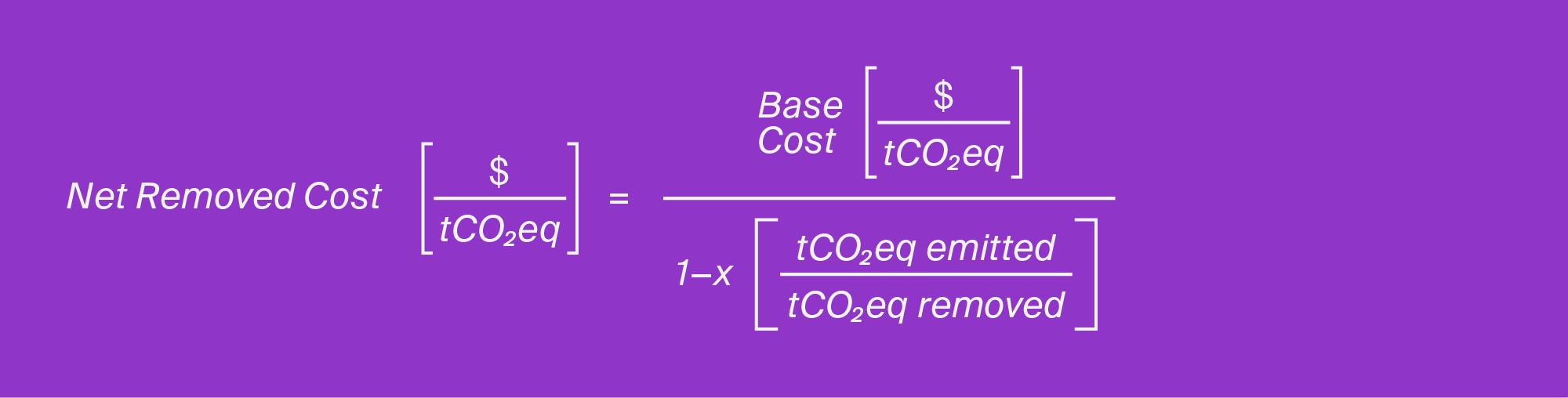
Here, we define variable x as the ratio of CO₂eq emitted to CO₂eq removed over the system life cycle. For this cost to reflect a CDR system, the CO₂eq emissions must be presented throughout the system life cycle, including subsequent storage or utilization. The denominator represents the net amount of CO₂eq removed from air per-tonne-CO₂eq captured from the air, if any. The numerator represents the total annualized cost of building and operating the CDR system on a per-tonne-CO₂eq-captured-from-air basis. Collectively, this expression gives the cost of the system per tonne of CO₂eq net removed from the air. The net removed cost is the estimated cost of reducing atmospheric CO₂eq concentration by 1 tonne. Note that as the amount of CO₂eq emitted approaches the amount of the CO₂eq removed, the net removed cost approaches infinity. For negative values of 1 – x, or for x values greater than 1, the system does not reduce emissions and, therefore, is not a CDR system. 

To develop and deploy CDR approaches at the scale necessary to meet climate goals will require insight into the environmental impact of those approaches, as well as their technical and economic feasibility. If used correctly, both LCA and TEA can provide systematic methods for evaluating existing and emerging CDR approaches, while playing a large role in how we define net-negative emissions for CDR systems.

We also stress that LCA and TEA are just components of the decision process around CDR deployment. Careful consideration of impacts outside of carbon accounting (environmental, social, economic, and political) are both critical and rarely as straightforward to quantify as LCA and TEA. This challenge creates an opportunity to integrate the social sciences more fully into technical assessments.